Coding is the closest thing we have to a surperpower
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 n 元钱就行”。今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
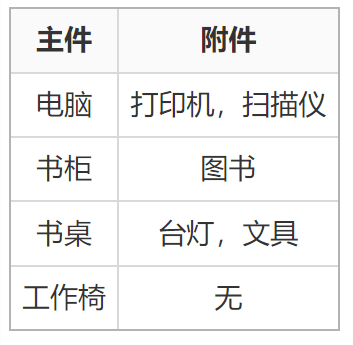
如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 0 个、1 个或 2 个附件。每个附件对应一个主件,附件不再有从属于自己的附件。金明想买的东西很多,肯定会超过妈妈限定的 n 元。于是,他把每件物品规定了一个重要度,分为 5 等:用整数 1∼5 表示,第 5 等最重要。他还从因特网上查到了每件物品的价格(都是 10 元的整数倍)。他希望在不超过 n 元的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 j 件物品的价格为 v_j,重要度为w_j,共选中了 k 件物品,编号依次为 j_1,j_2,\dots,j_k,则所求的总和为:
v_{j_1} \times w_{j_1}+v_{j_2} \times w_{j_2}+ \dots +v_{j_k} \times w_{j_k}
请你帮助金明设计一个满足要求的购物单。
第一行有两个整数,分别表示总钱数 n 和希望购买的物品个数 m。
第 2 到第 (m + 1) 行,每行三个整数,第 (i + 1) 行的整数 v_i,p_i,q_i 分别表示第 i 件物品的价格、重要度以及它对应的的主件。如果 q_i=0,表示该物品本身是主件。
对于全部的测试点,保证 1 \leq n \leq 3.2 \times 10^4,1 \leq m \leq 60,0 \leq v_i \leq 10^4,1 \leq p_i \leq 5,0 \leq q_i \leq m,答案不超过 2 \times 10^5。
输出一行一个整数表示答案。
输入
1000 5 800 2 0 400 5 1 300 5 1 400 3 0 500 2 0
输出
2200