test 8
A. 标准身材
易错点:
- 读题不仔细,没有看到单位不同(斤和千克)。
- 浮点数运算没开double。
- 不理解±10%内应该怎么表示。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
double h,w;
cin>>h>>w;
double bz=(h-100)*0.9*2; //注意将千克转换为斤,需要*2
if(bz*0.9<w&&w<bz*1.1) cout<<"GOOD\n";
else if(w>=bz*1.1) cout<<"OVERWEIGHT\n";
else if(w<=bz*0.9) cout<<"UNDERWEIGHT\n";
}
return 0;
}
B. 出入许可
练习题:2030
70分做法:
定义数组sum,sum[i]表示在i时刻申请出入许可,有多少项办公计划可被满足。
因为要在t时刻进出校门,所以出入许可应该在 t-k-c+1 ~ t-k 这个范围内申请,故可以枚举这个范围内的数,并令对应的sum++。
最后回答询问时,输出sum[q]即可。
#include<bits/stdc++.h>
using namespace std;
const int N = 1000010;
int n,m,k;
int sum[N]; //sum[i]表示在i时刻申请出入许可,有多少项办公计划可被满足
int main()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
{
int t,c;
cin>>t>>c;
//因为要在t时刻进出校门,所以出入许可应该在 t-k-c+1 ~ t-k这个范围内申请
//注意数组不能越界
for(int j=t-k-c+1;j<=t-k;j++) if(j>=1) sum[j]++;
}
for(int i=1;i<=m;i++)
{
int x;
cin>>x;
cout<<sum[x]<<endl;
}
return 0;
}
100分做法:
注意到上一份代码中计算sum数组时,实际上是对区间内的每一个元素+1,所以可以考虑用差分来优化时间复杂度,即将区间+1这个操作转化为差分数组的左端点+1,右端点后一位-1,最后再将差分数组求前缀和,即可得到与70分做饭相同的sum数组。
#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
int n,m,k;
int cf[N],sum[N];
//对差分数组求前缀和,便可以得到i这个时间申请出入许可能满足多少个办公计划
int maxr;
//maxr表示与sum数组相关的最晚的时间
int main()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
{
int t,c;
cin>>t>>c;
//因为要在t时刻进出校门,所以出入许可应该在 t-k-c+1 ~ t-k这个范围内申请
int l=t-k-c+1,r=t-k;
if(r>0)
{
cf[max(1,l)]++;
cf[r+1]--;
maxr=max(maxr,r+1);
}
}
for(int i=1;i<=maxr;i++) sum[i]=sum[i-1]+cf[i];
for(int i=1;i<=m;i++)
{
int x;
cin>>x;
cout<<sum[x]<<endl;
}
return 0;
}
C. 岛与字符串
练习题:2410
此题是动态规划中的经典题目,与最长公共子序列那道题类似,我们可以用一个二维dp数组来解决问题。
dp[i][j]表示将字符串A的前i个元素和字符串B的前j个元素变为相同字符串的最少字符操作次数,一开始时可以将整个数组赋极大值。
- 初始化:显然dp[0][j]=j,dp[i][0]=i
- 考虑状态转移的三种操作:具体见代码注释。
#include <bits/stdc++.h>
using namespace std;
const int inf=0x7f7f7f7f;
string s1,s2;//初始字符串
int l1,l2;
int dp[2010][2010];
//dp[i][j]表示将字符串A的前i个元素和字符串B的前j个元素变为相同字符串的最少字符操作次数
int main()
{
cin>>s1>>s2;
l1=s1.length();
l2=s2.length();
// 初始化dp数组为极大值
for(int i=0;i<=l1;i++) for(int j=0;j<=l2;j++) dp[i][j]=inf;
for(int i=0;i<=l1;i++) dp[i][0]=i;
for(int i=0;i<=l2;i++) dp[0][i]=i;
for(int i=1; i<=l1;i++)
{
for(int j=1;j<=l2;j++)
{
if(s1[i-1]==s2[j-1]) //如果两位相同,那么不需要增加次数
dp[i][j]=min(dp[i][j],dp[i-1][j-1]);
else //否则,需要将一个字符换为另一个字符,次数+1
dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);
// 添加一个字符,即在字符串A中加入s2[j-1]这个字符
dp[i][j]=min(dp[i][j],dp[i][j-1]+1);
// 删除一个字符,即删除字符串A中的s1[i-1]这个字符
dp[i][j]=min(dp[i][j],dp[i-1][j]+1);
}
}
cout<<dp[l1][l2]<<endl;
return 0;
}
D.英雄传说
练习题:[NOIP2017 提高组] 奶酪
看到距离魔物的最短距离最长,可以立刻想到二分答案,问题在于如何判断是否存在距离魔物的最短距离>=mid的路径。
由于英雄不一定要走在整点上,所以传统的以英雄为中心的搜索显然是不可行的,需要变换一下思路。考虑把距离魔物的最短距离>=mid这件事看做魔物的占领区域是一个以魔物为中心,半径为mid的圆,其中圆的内部是不能走的,但边界可以走。那么如果魔物们的占领区域相交,堵住了从(1,1)走向(n,n)的路,那么就不存在这样的路径了。
可以通过简单的画图来理解什么情况下会堵住从(1,1)走向(n,n)的路,有以下四种情况:
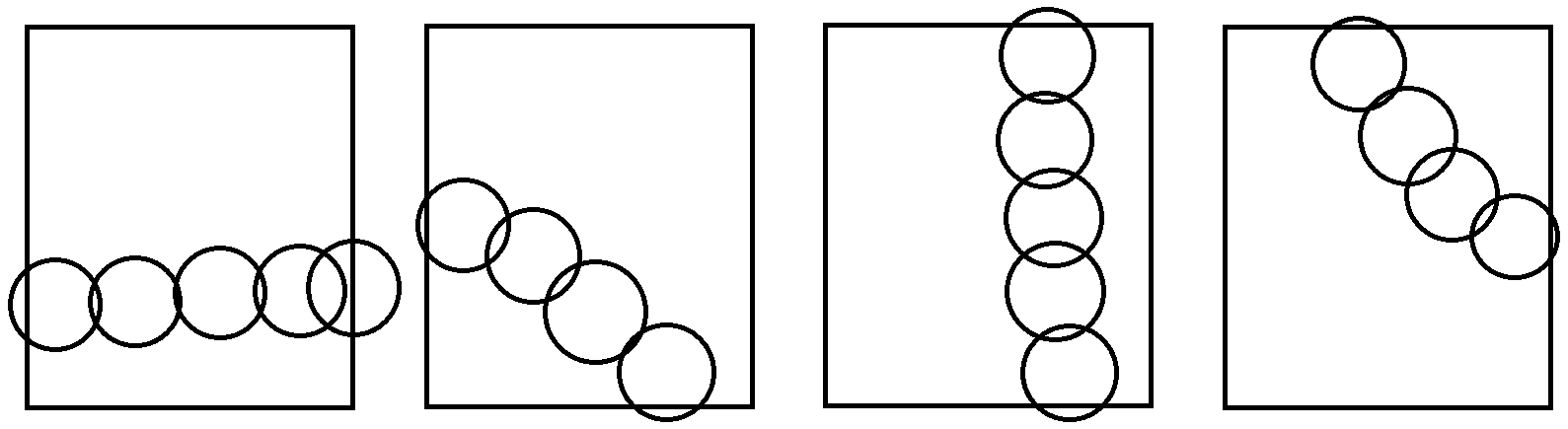
其中圆圈表示魔物的占领区,这些圆圈的半径是相同的。可以发现如果几个占领区相交,且与地图边界相交,那么就有可能堵住从(1,1)走向(n,n)的路,英雄就不能走过去了。
观察这四种情况,可以发现,将所有与左边界或上边界连通的魔物作为起点,如果从它们开始可以走到与右边界或下边界连通的魔物,那么就可以堵住路了。判断从一个魔物是否与另一个魔物相交也比较简单 ,只需要计算两个魔物之间的距离,判断距离是否<2*mid即可。
#include<bits/stdc++.h>
using namespace std;
int dis[3001][3001]; //距离的平方
int x[3001],y[3001];
int getdis(int x1,int y1,int x2,int y2)
{
return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
}
bool able(int d,double r)
// 判断d与2r的大小关系,如果小于,则证明这两个魔物占领的范围相交
// 相切的情况不能考虑,因为相切时英雄是可以通过的
// 由于保存的dis是距离的平方,所以2r也要平方
{
return d < (2*r)*(2*r);
}
int m,n,k;
queue<int> q;
bool vis[3001];
bool bfs(double r) //判断是否存在距离魔物的最短距离>=r的路径
{
//清空数组
memset(vis,0,sizeof(vis));
while(!q.empty()) q.pop();
for(int i=1; i<=k; i++)
{
if(x[i]-1<r||m-y[i]<r) //将所有与左边界或上边界连通的魔物加入队列中
// x[i]-1是因为边界为1,所以和1的距离<r即可
{
q.push(i);
vis[i]=1;
}
}
while(!q.empty())
{
int u=q.front();
q.pop();
// 如果当前的魔物能与右边界或下边界连通,则能阻挡住英雄的去路
if(n-x[u]<r||y[u]-1<r) return 0;
for(int i=1; i<=k; i++)
{
if(!vis[i]&&able(dis[u][i],r))
{
vis[i]=1;
q.push(i);
}
}
}
return 1;
}
int main()
{
cin>>k>>n>>m;
for(int i=1; i<=k; i++) cin>>x[i]>>y[i];
//求出魔物两两间的距离
for(int i=1; i<=k; i++)
for(int j=1; j<i; j++)
dis[i][j]=dis[j][i]=getdis(x[i],y[i],x[j],y[j]);
double l=0,r=min(m,n),mid; //二分答案
while(r-l>=1e-6)
{
mid=(l+r)/2;
if(bfs(mid)) l=mid; //用bfs找是否存在
else r=mid;
}
printf("%.2lf",l);
return 0;
}