给定一个有向图，N个顶点，M条边，顶点从1到N编号，每个顶点上有金币g_1, g_2, g_3, ..., g_N​，有P个休息站r_1, r_2, r_3, ..., r_P​。

现在要求从S号顶点出发，对顶点进行金币收集，最后要求停留在某个休息站，问最多可以收集多少金币。

例如， 6 个顶点，道路的连接情况如下图所示：

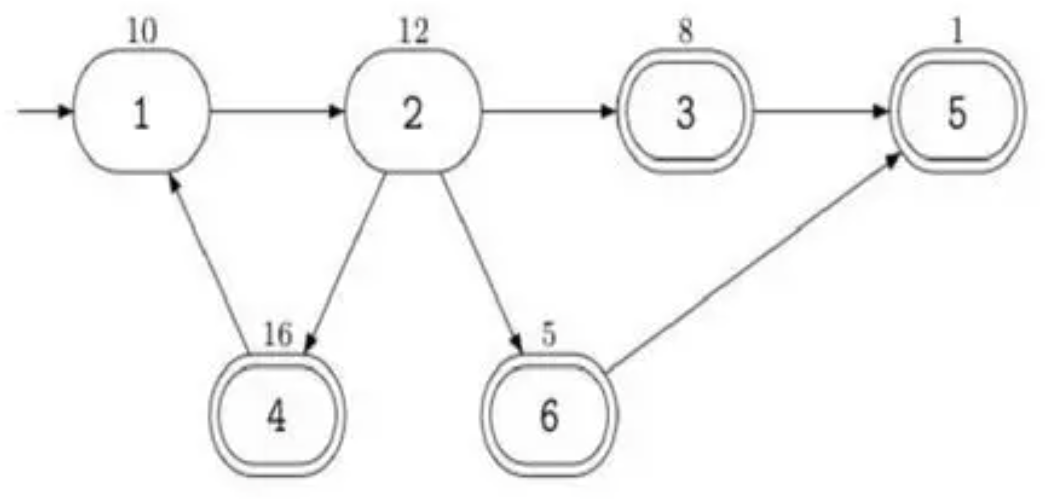
现在从1号顶点出发，休息站用双圈来表示。每个顶点的金币数显示在该顶点上方。

在这个例子中，最多可收集47个金币，实施的路线是：1-2-4-1-2-3-5。

第一行包含两个整数N, M (1 \le N, M \le 5*10^5)。

接下来M行，每行两个整数u, v (0 \le u, v \le N)，表示u到v有一条单向路径。

接下来一行N个整数g_1, g_2, g_3, ..., g_N( 0 \le g_i \le 4000)，按g_i表示第i个顶点的金币数目。

接下来一行包含两个整数S, P(1 \le S, P \le N)。

接下来的一行有P个整数r_1, r_2, r_3, ..., r_P(1 \le r_i \le N)，表示P个休息站的编号。

输入数据保证你可以从S到达至少一个休息站。

输出最多可以收集的金币数目。