一个 m \times n 的矩阵是一个由 m 行 n 列元素排列成的矩形阵列。即形如：

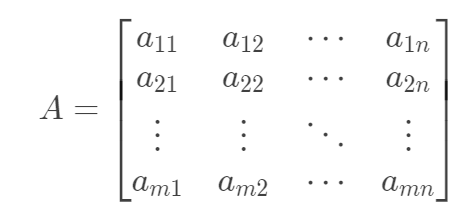
本题中认为矩阵中的元素 a_{i j} 是整数。 
两个大小分别为 m \times n 和 n \times p 的矩阵 A, B 相乘的结果为一个大小为 m \times p 的矩阵。将结果矩阵记作 C，则：

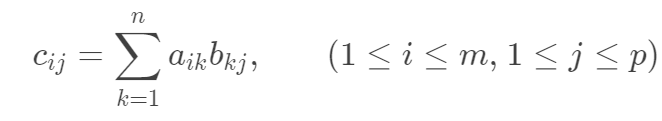
而如果 A 的列数与 B 的行数不相等，则无法进行乘法。 

可以验证，矩阵乘法满足结合律，即 (A B) C = A (B C)。 

一个大小为 n \times n 的矩阵 A 可以与自身进行乘法，得到的仍是大小为 n \times n 的矩阵，记作 A^2 = A \times A。进一步地，还可以递归地定义任意高次方 A^k = A \times A^{k - 1}。

特殊地，定义 A^0 为单位矩阵 I = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix}。 

这道题的要求为：给定 n\times n 的矩阵 A，求 A^k。 

第一行两个整数 n,k。   
接下来 n 行，每行 n 个整数，第 i 行的第 j 的数表示 A_{i,j}。 

对于 100\% 的数据，1\le n \le 100，0 \le k \le 10^{12}，|A_{i,j}| \le 1000。

输出 A^k ，共 n 行，每行 n 个数，第 i 行第 j 个数表示 (A^k)_{i,j}，每个元素对 10^9+7 取模。